Gravitation and General Relativity
What is gravity, the term we're all used to? what do we know about it, and what remains unknown? How did Einstein make huge contributions to this field? What does Relativity talk about? Find out the answers to all these questions here, in this article.
History of gravity
So there was this Danish nobleman and astronomer, named Tycho Brahe. He made a lot of pretty accurate observations (considering the epoch and the limited technology available during that time) regarding the positions of planets and their orbits. He had this student named Johannes Kepler, who would later become very famous by the laws named "Kepler's planetary laws". He presented three laws, concerning the speed and positions of planets in the solar system, based on Tycho Brahe's observations.
Then came our lovely old friend - Sir Isaac Newton. Using Kepler's laws, observations, and of course his intellect, Newton formulated the universal law of gravitation, declaring that the gravitational force between any two objects in space is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This was revolutionary because of the fact that it suggested the same law holds for celestial objects and objects on earth, contrary to what was believed before this.
Newtonian Gravity
I have already mentioned the statement of Newton's universal law of gravitation above. This law suggested that gravity is a "force at a distance" concept, wherein the two interacting bodies do not have any physical contact with each other. This is very counter-intuitive and in Newton's own words,
"That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
Which basically says that it does not make sense for two bodies to interact with one another without any contact. This was later rectified by Einstein, who predicted that gravitation is a field, and it is the field that interacts with the body. I'll discuss more on it in a minute.
Problems with Newtonian gravity:
1. It had been observed that the orbit of Mercury is spinning at a rate of 43 arcseconds per century. But, Newton's theory could not explain this and thus failed here.
2. In Spiral galaxies, the orbiting stars do not seem to obey Newton's laws. - Another drawback.
And there are more drawbacks, which I'd rather not discuss right now.
But one thing was clear - some modifications were required in Newton's theory, though it satisfactorily explained most of the stuff.
The equivalence principle
Described as the happiest thought of Einstein's life, the equivalence principle basically describes gravitation as any other force, i.e., in terms of acceleration and deceleration. You'll understand that by reading the following mind experiment:
Consider two observers: A and B. A is in a cabin on Earth, while B is in another identical cabin, that is outside the earth in free space (there is no force acting on this observer). Now, imagine that both A and B are provided with identical balls. If A drops the ball in his cabin, he'll say that the acceleration of the ball is 9.8 m/s^2. Now imagine that the cabin in which B is present moves upwards with an acceleration of 9.8m/s^2. Now, since B as an observer always consider himself to be at rest, he will notice that the ball that was initially floating in his cabin is now pulled downwards and "falls" down with an acceleration of 9.8m/s^2. There is no mechanical experiment through which B can decide if he is on earth or in free space.
This essentially is the Equivalence principle, that the gravitational mass of a body(measured by A) is equal to the inertial mass(measured by B).
Note: i) just in case you're wondering why I termed the mass measured by B inertial, the reason is as follows: the ball wants to stay where it was, as there is no force acting on the ball. but for B, some "pseudo" force is pulling the ball downwards.
ii) If you're confused about why I first talked about accelerations and then brought in mass, there is actually a more detailed way of proving the equivalence principle, which I will exclude here to keep this article as simple as I can.
A very brief introduction to General Relativity
Yes, it is one of the most difficult to understand topics in Physics, and that's why I'll only touch the topic in the following lines, keeping things as simple as I can.
If you've read my other article on spacetime(if you haven't, check it out: Spacetime, Time Travel, and Dilation, Relativity) you'll have an idea about what it is. So General Relativity describes Gravitation as a ripple or disturbance of spacetime, as it passes from one body to another.
Now, let me introduce you to the concept of geodesics. Imagine throwing a ball in free space; it will go in a straight line, right? Now imagine throwing a ball horizontally near the surface of the earth. I'm pretty sure we all have the experience that this ball will go in a curved path with respect to us. But look at it this way: As I've mentioned before, masses curve the geometry of spacetime. So the ball that we throw horizontally on the surface of the earth, follows the spacetime geometry that was curved by the earth. If there were no earth at this particular position, the spacetime would be flat, and the ball would've gone in a straight-line path. But putting the earth bends the spacetime at that region, and hence changes the path of the ball accordingly.
So now, I claim that the ball essentially goes in a straight line in the direction of the spacetime at that instant of region and time. This path, that was curved by the presence of matter, is known as a geodesic. And just like Newton's first law, Einsteins Equations also say that if I apply a force on this ball moving on the path, the ball would deviate from its initial geodesic, and would now follow a spacetime geodesic that is the resultant of both the Earth's gravitational force and the force exerted from my hand.
Using some basic principles, advanced maths, tensors, and other stuff, Einstein derived a set of 10 differential equations known as Einstein's Field Equations, which tell us about the geometry of spacetime at particular places and times and presence of forces.
The success of Einstein's Theory
Although a bit abstract and difficult to understand, Einstein's theory of general relativity has met tremendous success. It can be used wherever Newton's theory seems inadequate. Here are a few cool things about General Relativity:
1. Black holes were predicted by Einstein's Field Equations(E.F.E). The radius of a stationary black hole calculated from E.F.E is known as Schwarzschild Radius.
2. General Relativity predicts that Gravitation propagates through waves, which was only recently confirmed by LIGO(more than 100 years after General relativity was published)
3. It accurately describes the bending of light around the sun and/or any other massive object.
4. It calculates the precession of Mercury's orbit(I mentioned about this in Newtonian Gravity's drawbacks)
5. Satellites extensively use General Relativity.
The only problem with General Relativity and E.F.E is that the 10 differential equations are very difficult to solve. So, in places where we don't need accuracy to a very high level, Newtonian Formula is used owing to its simplicity.
For more such articles/topics, visit https://theuniversebeauty.blogspot.com/
History of gravity
 |
| This is where Kepler presented his first two laws. credits: http://www.sothebys.com/ |
Then came our lovely old friend - Sir Isaac Newton. Using Kepler's laws, observations, and of course his intellect, Newton formulated the universal law of gravitation, declaring that the gravitational force between any two objects in space is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This was revolutionary because of the fact that it suggested the same law holds for celestial objects and objects on earth, contrary to what was believed before this.
 |
| Newton's Gravitation Mathematical formula Image credits: Science photo library |
I have already mentioned the statement of Newton's universal law of gravitation above. This law suggested that gravity is a "force at a distance" concept, wherein the two interacting bodies do not have any physical contact with each other. This is very counter-intuitive and in Newton's own words,
"That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
Which basically says that it does not make sense for two bodies to interact with one another without any contact. This was later rectified by Einstein, who predicted that gravitation is a field, and it is the field that interacts with the body. I'll discuss more on it in a minute.
Problems with Newtonian gravity:
1. It had been observed that the orbit of Mercury is spinning at a rate of 43 arcseconds per century. But, Newton's theory could not explain this and thus failed here.
2. In Spiral galaxies, the orbiting stars do not seem to obey Newton's laws. - Another drawback.
And there are more drawbacks, which I'd rather not discuss right now.
But one thing was clear - some modifications were required in Newton's theory, though it satisfactorily explained most of the stuff.
The equivalence principle
Described as the happiest thought of Einstein's life, the equivalence principle basically describes gravitation as any other force, i.e., in terms of acceleration and deceleration. You'll understand that by reading the following mind experiment:
 |
| Figurative explanation of the Equivalence principle. |
This essentially is the Equivalence principle, that the gravitational mass of a body(measured by A) is equal to the inertial mass(measured by B).
Note: i) just in case you're wondering why I termed the mass measured by B inertial, the reason is as follows: the ball wants to stay where it was, as there is no force acting on the ball. but for B, some "pseudo" force is pulling the ball downwards.
ii) If you're confused about why I first talked about accelerations and then brought in mass, there is actually a more detailed way of proving the equivalence principle, which I will exclude here to keep this article as simple as I can.
A very brief introduction to General Relativity
Yes, it is one of the most difficult to understand topics in Physics, and that's why I'll only touch the topic in the following lines, keeping things as simple as I can.
If you've read my other article on spacetime(if you haven't, check it out: Spacetime, Time Travel, and Dilation, Relativity) you'll have an idea about what it is. So General Relativity describes Gravitation as a ripple or disturbance of spacetime, as it passes from one body to another.
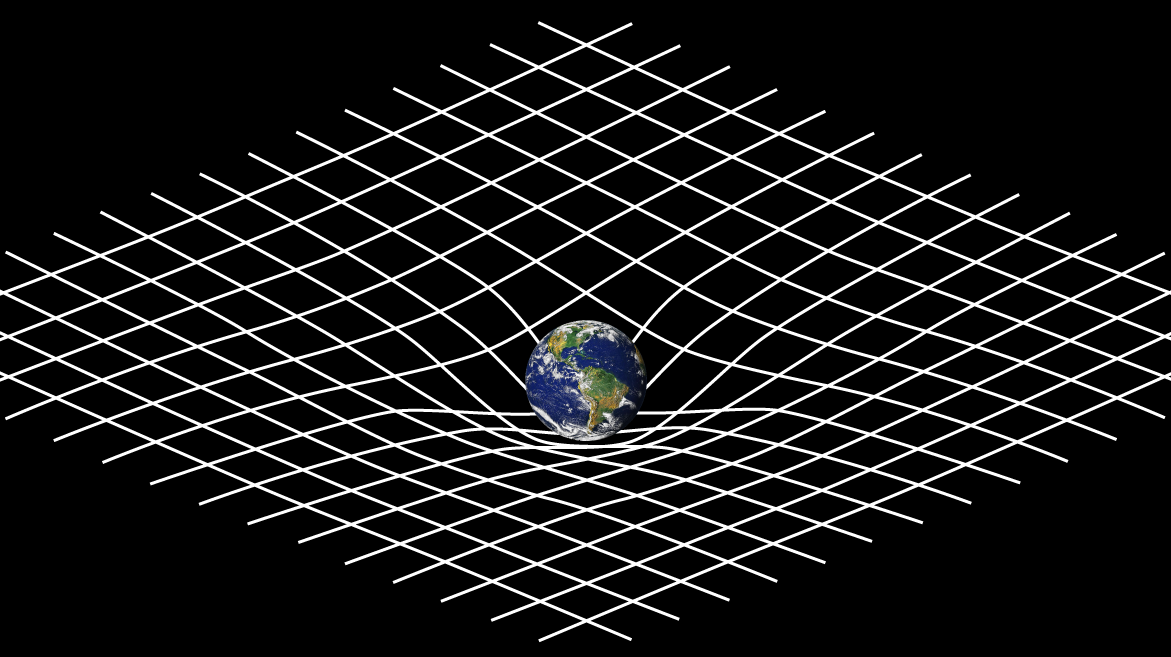 |
| Image credits: NASA |
So now, I claim that the ball essentially goes in a straight line in the direction of the spacetime at that instant of region and time. This path, that was curved by the presence of matter, is known as a geodesic. And just like Newton's first law, Einsteins Equations also say that if I apply a force on this ball moving on the path, the ball would deviate from its initial geodesic, and would now follow a spacetime geodesic that is the resultant of both the Earth's gravitational force and the force exerted from my hand.
Using some basic principles, advanced maths, tensors, and other stuff, Einstein derived a set of 10 differential equations known as Einstein's Field Equations, which tell us about the geometry of spacetime at particular places and times and presence of forces.
| Einstein's field equations. Image credits: Facebook |
The success of Einstein's Theory
Although a bit abstract and difficult to understand, Einstein's theory of general relativity has met tremendous success. It can be used wherever Newton's theory seems inadequate. Here are a few cool things about General Relativity:
1. Black holes were predicted by Einstein's Field Equations(E.F.E). The radius of a stationary black hole calculated from E.F.E is known as Schwarzschild Radius.
2. General Relativity predicts that Gravitation propagates through waves, which was only recently confirmed by LIGO(more than 100 years after General relativity was published)
3. It accurately describes the bending of light around the sun and/or any other massive object.
4. It calculates the precession of Mercury's orbit(I mentioned about this in Newtonian Gravity's drawbacks)
5. Satellites extensively use General Relativity.
The only problem with General Relativity and E.F.E is that the 10 differential equations are very difficult to solve. So, in places where we don't need accuracy to a very high level, Newtonian Formula is used owing to its simplicity.
For more such articles/topics, visit https://theuniversebeauty.blogspot.com/
It is very well written and comprehensible. Great job!!
ReplyDeleteThanks
DeleteHi rikhil!! Finally found your blog
ReplyDeleteg1 man...beyond me ;)
ReplyDelete